Macaulay Duration
Macaulay Duration เป็นเครื่องมือใช้วัดความอ่อนไหวของราคาหุ้นกู้ต่อการเปลี่ยนแปลงของอัตราดอกเบี้ย โดยคำนวณจากค่าเฉลี่ยถ่วงน้ำหนักของระยะเวลาที่จะได้รับกระแสเงินสดในอนาคตของหุ้นกู้ ส่วนน้ำหนักคือมูลค่าปัจจุบันของกระแสเงินสดแต่ละงวดเทียบกับราคาหุ้นกู้ Macaulay Duration จึงแสดงถึงอายุเฉลี่ยของกระแสเงินสดของหุ้นกู้ มีสูตรคำนวณดังนี้
Source: https://analystprep.com/cfa-level-1-exam/fixed-income/macaulay-modified-effective-durations/
Modified Duration
Macaulay Duration มีข้อจำกัดในการวัดความเสี่ยงด้านอัตราดอกเบี้ย จึงมีการพัฒนา Modified Duration ขึ้น โดยคำนวณจาก Macaulay Duration หารด้วยหนึ่งบวกอัตราผลตอบแทนจนครบกำหนดไถ่ถอน (Yield to Maturity: YTM) Modified Duration ให้ค่าประมาณการเปลี่ยนแปลงของราคาหุ้นกู้เมื่ออัตราผลตอบแทนเปลี่ยนแปลงไป 1% มีสูตรคำนวณดังนี้
Source: https://analystprep.com/cfa-level-1-exam/fixed-income/macaulay-modified-effective-durations/
Effective Duration
แม้ Modified Duration จะให้ค่าประมาณการที่ดีขึ้น แต่ยังมีข้อจำกัดสำหรับหุ้นกู้ที่มีอนุพันธ์แฝง (Embedded Options) เช่น หุ้นกู้ที่ไถ่ถอนก่อนกำหนดได้ (Callable Bond) หรือหุ้นกู้ที่อ้างอิงสินเชื่อที่อยู่อาศัย (Mortgage-Backed Securities) เนื่องจากกระแสเงินสดในอนาคตของหุ้นกู้เหล่านี้ไม่แน่นอน ขึ้นอยู่กับการใช้สิทธิของผู้ออกหรือผู้ถือหุ้นกู้
ดังนั้นจึงมีการพัฒนา Effective Duration ขึ้นเพื่อวัดความเสี่ยงด้านอัตราดอกเบี้ยของหุ้นกู้ที่มีอนุพันธ์แฝงได้อย่างแม่นยำยิ่งขึ้น Duration ที่มีประสิทธิภาพคำนวณจากการเปลี่ยนแปลงของราคาหุ้นกู้เมื่ออัตราผลตอบแทนของหุ้นกู้อ้างอิง (Benchmark Yield Curve) เปลี่ยนแปลงไป โดยใช้แบบจำลองการกำหนดราคาหุ้นกู้ที่ซับซ้อนกว่า มีสูตรคำนวณดังนี้
Source: https://analystprep.com/cfa-level-1-exam/fixed-income/macaulay-modified-effective-durations/
ข้อได้เปรียบสำคัญของ Effective Duration คือสามารถคำนวณความอ่อนไหวของราคาหุ้นกู้ต่อการเปลี่ยนแปลงของ Yield Curve ทั้งเส้น ไม่ใช่เพียงการเปลี่ยนแปลงของอัตราผลตอบแทนจนครบกำหนดไถ่ถอนเท่านั้น ทำให้สามารถประเมินความเสี่ยงของหุ้นกู้ที่มีอนุพันธ์แฝงได้แม่นยำกว่า เนื่องจากมีการคำนึงถึงความไม่แน่นอนของกระแสเงินสดในอนาคต
นอกจากนี้ Effective Duration ยังแยกผลกระทบจากการเปลี่ยนแปลงของอัตราดอกเบี้ยอ้างอิงออกจากการเปลี่ยนแปลงของส่วนต่างอัตราผลตอบแทน (Yield Spread) ทำให้สามารถวิเคราะห์ความเสี่ยงด้านเครดิตและสภาพคล่องแยกออกจากความเสี่ยงด้านอัตราดอกเบี้ยได้ชัดเจนยิ่งขึ้น
อย่างไรก็ตาม Effective Duration ก็ยังมีข้อจำกัดบางประการ เช่น อาจให้ค่าที่คลาดเคลื่อนสำหรับการเปลี่ยนแปลงของอัตราดอกเบี้ยในระดับสูง หรือกรณีที่เส้นอัตราผลตอบแทนมีการเปลี่ยนแปลงรูปร่างอย่างมีนัยสำคัญ นักลงทุนจึงควรใช้ Effective Duration ร่วมกับเครื่องมืออื่นๆ เช่น การวิเคราะห์ความเสี่ยงแบบ Value at Risk (VaR) หรือการทดสอบภาวะวิกฤต (Stress Testing) เพื่อให้ได้ภาพรวมของความเสี่ยงที่สมบูรณ์ยิ่งขึ้น
สรุป
Effective Duration เป็นเครื่องมือที่มีประโยชน์ในการวัดและจัดการความเสี่ยงด้านอัตราดอกเบี้ยหุ้นกู้ โดยเฉพาะหุ้นกู้ที่มีอนุพันธ์แฝง ช่วยให้นักลงทุนและผู้จัดการกองทุนสามารถตัดสินใจลงทุนและบริหารความเสี่ยงได้อย่างมีประสิทธิภาพมากขึ้น ในยุคที่ตลาดการเงินมีความผันผวนสูงและผลิตภัณฑ์ทางการเงินมีความซับซ้อนเพิ่มขึ้น การพัฒนาเครื่องมือวัดความเสี่ยงให้มีความแม่นยำและครอบคลุมยิ่งขึ้นจึงมีความสำคัญอย่างยิ่งต่อเสถียรภาพของระบบการเงินโดยรวม





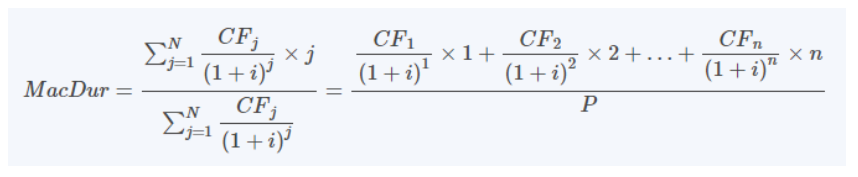
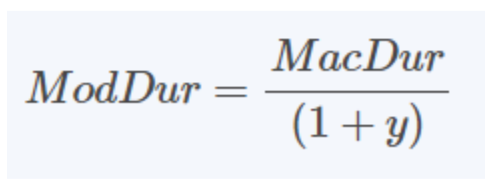
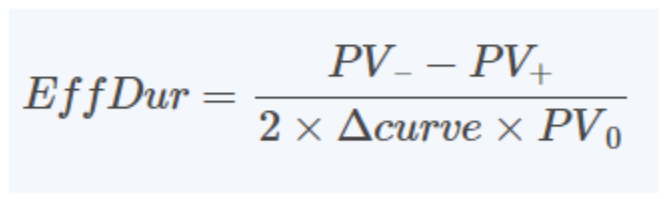





![ทฤษฎี Elliott Wave (อีเลียตเวฟ) คืออะไร [แบบละเอียด] ทฤษฎี Elliott Wave](https://www.lucid-trader.com/wp-content/uploads/2020/12/ทฤษฎี-Elliott-Wave-218x150.png)

![ทฤษฎี Wyckoff Logic คืออะไร [แบบละเอียด] Wyckoff Logic](https://www.lucid-trader.com/wp-content/uploads/2020/10/Wyckoff-Logic-218x150.png)