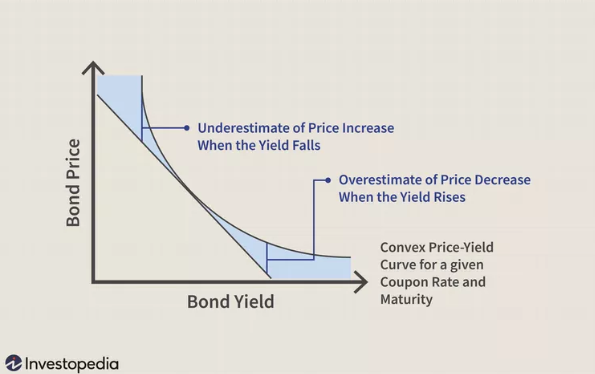
Bond Convexity
เป็นการวัดอัตราการเปลี่ยนแปลงของ duration ของหุ้นกู้เมื่อผลตอบแทนเปลี่ยนแปลงไป โดยทั่วไปเส้นความสัมพันธ์ระหว่างราคาและผลตอบแทนของหุ้นกู้จะมีลักษณะโค้งเว้าเข้าหาจุดกำเนิด ซึ่งหมายความว่าเมื่อผลตอบแทนลดลง ราคาหุ้นกู้จะเพิ่มขึ้นในอัตราที่เร็วกว่าอัตราการลดลงของราคาเมื่อผลตอบแทนเพิ่มขึ้นในปริมาณที่เท่ากัน
Source: https://www.investopedia.com/articles/bonds/08/duration-convexity.asp
การคำนวณความโค้งโดยประมาณสามารถทำได้โดยใช้สูตร:
Convexity = (V+ + V- – 2V0) / ((ΔYTM)^2 * V0)
โดยที่ V+, V-, V0 คือมูลค่าหุ้นกู้ที่ผลตอบแทนเพิ่มขึ้น ลดลง และไม่เปลี่ยนแปลงตามลำดับ ΔYTM คือการเปลี่ยนแปลงของผลตอบแทน
สำหรับหุ้นกู้ที่มี option แฝง เช่น หุ้นกู้ที่สามารถไถ่ถอนก่อนกำหนดได้ (Callable Bond) จะต้องใช้ Effective Convexity แทน โดยคำนวณจากการเปลี่ยนแปลงของ Yield Curve แทนการเปลี่ยนแปลงของ YTM
ปัจจัยที่มีผลต่อความโค้งของหุ้นกู้ ได้แก่ อายุคงเหลือ อัตราดอกเบี้ยคูปอง และอัตราผลตอบแทน โดยหุ้นกู้ที่มีอายุยาวกว่า อัตราดอกเบี้ยคูปองต่ำกว่า หรือผลตอบแทนต่ำกว่า จะมีความโค้งมากกว่า
การประมาณการเปลี่ยนแปลงของราคาหุ้นกู้
การประมาณการเปลี่ยนแปลงของราคาหุ้นกู้เมื่อผลตอบแทนเปลี่ยนแปลงไปสามารถทำได้โดยใช้ทั้ง duration และ convexity ดังนี้:
การเปลี่ยนแปลงของราคาหุ้นกู้ (%) = -Modified Duration * ΔYTM + 1/2 * Convexity * (ΔYTM)^2
โดยพจน์แรกคือผลกระทบอันดับหนึ่ง (First-order Effect) และพจน์ที่สองคือผลกระทบอันดับสอง (Second-order Effect) ซึ่งช่วยให้การประมาณการมีความแม่นยำมากขึ้น โดยเฉพาะเมื่อการเปลี่ยนแปลงของผลตอบแทนมีขนาดใหญ่
ตัวอย่างเช่น หุ้นกู้ราคา 908 บาท ผลตอบแทน 9% Duration 9.42 ปี และ Convexity 68.33 เมื่อผลตอบแทนเพิ่มขึ้น 30 basis points ผลกระทบจาก Duration = -9.42 * 0.003 = -2.826% ผลกระทบจาก Convexity = 1/2 * 68.33 * (0.003)^2 = 0.0307% ราคาหุ้นกู้จะลดลงประมาณ 2.7953%
ความผันผวนของผลตอบแทน (Yield Volatility)
ความผันผวนของผลตอบแทนหมายถึงความสัมพันธ์ระหว่างความผันผวนของอัตราผลตอบแทนหุ้นกู้กับระยะเวลาครบกำหนด โดยความอ่อนไหวของราคาหุ้นกู้ต่อการเปลี่ยนแปลงของผลตอบแทนขึ้นอยู่กับ duration และ convexity ของหุ้นกู้
ในทางปฏิบัติ การเปลี่ยนแปลงของเส้นผลตอบแทนมักไม่ได้เป็นแบบขนานเสมอไป เช่น นโยบายการเงินอาจส่งผลต่ออัตราดอกเบี้ยระยะสั้นมากกว่าระยะยาว ดังนั้นหุ้นกู้ระยะสั้นอาจมีความผันผวนของราคามากกว่าหุ้นกู้ระยะยาวที่มี Duration สูงกว่าก็ได้ เนื่องจากความผันผวนของผลตอบแทนระยะสั้นมีมากกว่า
ความสัมพันธ์ระหว่างผลตอบแทนการถือครอง ระยะเวลาการลงทุน และ Duration
Macaulay Duration มีประโยชน์ในการจับคู่หุ้นกู้กับระยะเวลาการลงทุนของนักลงทุน โดยเมื่อระยะเวลาการลงทุนเท่ากับ Macaulay Duration ของหุ้นกู้ การเปลี่ยนแปลงของเส้นผลตอบแทนก่อนงวดจ่ายดอกเบี้ยแรกจะไม่ส่งผลกระทบ (หรือส่งผลน้อยมาก) ต่อผลตอบแทนการถือครองของนักลงทุน
สำหรับนักลงทุนที่มีระยะเวลาการลงทุนสั้นกว่า Macaulay Duration ของหุ้นกู้ ความเสี่ยงด้านราคาตลาดจะมีน้ำหนักมากกว่าความเสี่ยงจากการนำเงินไปลงทุนใหม่ โดยการเพิ่มขึ้นของผลตอบแทนก่อนวันจ่ายดอกเบี้ยงวดแรกจะทำให้ผลตอบแทนการถือครองลดลง ในทางกลับกัน หากผลตอบแทนลดลง นักลงทุนระยะสั้นจะได้รับผลกำไรจากราคาที่เพิ่มขึ้นและมีผลตอบแทนการถือครองสูงกว่าผลตอบแทนเริ่มต้นของหุ้นกู้
สำหรับนักลงทุนที่มีระยะเวลาการลงทุนยาวกว่า Macaulay Duration ของหุ้นกู้ การเพิ่มขึ้นของผลตอบแทนจะส่งผลให้รายได้จากการนำเงินไปลงทุนใหม่เพิ่มขึ้นมากกว่าการลดลงของราคาขายหุ้นกู้ ทำให้ผลตอบแทนการถือครองสูงขึ้น ในทางกลับกัน หากผลตอบแทนลดลง นักลงทุนระยะยาวจะได้รับผลกระทบจากรายได้จากการนำเงินไปลงทุนใหม่ที่ลดลง ทำให้ผลตอบแทนการถือครองต่ำกว่าผลตอบแทนเริ่มต้นของหุ้นกู้
ความแตกต่างระหว่าง Macaulay Duration ของหุ้นกู้กับระยะเวลาการลงทุนของนักลงทุนเรียกว่า Duration Gap โดย Duration Gap เป็นบวก (Macaulay Duration มากกว่าระยะเวลาการลงทุน) จะทำให้นักลงทุนมีความเสี่ยงด้านราคาตลาดจากการที่อัตราดอกเบี้ยเพิ่มขึ้น ในขณะที่ Duration Gap เป็นลบ (Macaulay Duration น้อยกว่าระยะเวลาการลงทุน) จะทำให้นักลงทุนมีความเสี่ยงจากการนำเงินไปลงทุนใหม่เมื่ออัตราดอกเบี้ยลดลง
สรุป
ความเข้าใจเกี่ยวกับความสัมพันธ์ระหว่างราคาและผลตอบแทนของหุ้นกู้ รวมถึงแนวคิดเรื่องความโค้งและความผันผวนของผลตอบแทน จะช่วยให้นักลงทุนสามารถประเมินมูลค่าและความเสี่ยงของหุ้นกู้ได้อย่างแม่นยำมากขึ้น ซึ่งเป็นประโยชน์ในการตัดสินใจลงทุนและบริหารความเสี่ยงของพอร์ตการลงทุนในตราสารหนี้










![ทฤษฎี Elliott Wave (อีเลียตเวฟ) คืออะไร [แบบละเอียด] ทฤษฎี Elliott Wave](https://www.lucid-trader.com/wp-content/uploads/2020/12/ทฤษฎี-Elliott-Wave-218x150.png)

![ทฤษฎี Wyckoff Logic คืออะไร [แบบละเอียด] Wyckoff Logic](https://www.lucid-trader.com/wp-content/uploads/2020/10/Wyckoff-Logic-218x150.png)